[LeetCode] 773. Sliding Puzzle 滑动拼图

On an 2 x 3 board, there are five tiles labeled from 1 to 5, and an empty square represented by 0. A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.

The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].

Given the puzzle board board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.

Example 1:

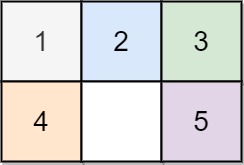
Input: board = [[1,2,3],[4,0,5]]
Output: 1
Explanation: Swap the 0 and the 5 in one move.

Example 2:

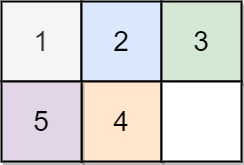
Input: board = [[1,2,3],[5,4,0]]
Output: -1
Explanation: No number of moves will make the board solved.

Example 3:

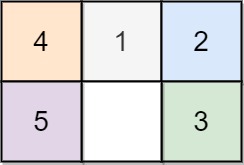
Input: board = [[4,1,2],[5,0,3]]
Output: 5
Explanation: 5 is the smallest number of moves that solves the board.
An example path:
After move 0: [[4,1,2],[5,0,3]]
After move 1: [[4,1,2],[0,5,3]]
After move 2: [[0,1,2],[4,5,3]]
After move 3: [[1,0,2],[4,5,3]]
After move 4: [[1,2,0],[4,5,3]]
After move 5: [[1,2,3],[4,5,0]]

Example 4:

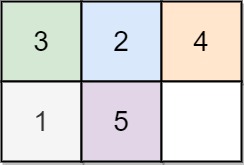
Input: board = [[3,2,4],[1,5,0]]
Output: 14

Constraints:

board.length == 2
board[i].length == 3
0 <= board[i][j] <= 5
Each value board[i][j] is unique.

看到这道题不禁让博主想起了文曲星上的游戏-华容道，好吧，又暴露年龄了|||-.-，貌似文曲星这种电子辞典神马的已经是很古老的东西了，但是上面的一些经典游戏，什么英雄坛说啊，华容道啊，虽然像素分辨率低的可怜，画面效果连小霸王学习机其乐无穷都比不上，更不要说跟现在的什么撸啊撸，吃鸡之类的画面相比了，但是却给初高中时代的博主学习之余带来了无限的乐趣。不过这题跟华容道还是有些不同的，因为那个游戏各块的大小不同，而这道题的拼图大小都是一样的。那么像这种类似迷宫遍历的问题，又要求最小值的问题，要有强烈的 BFS 的感觉，没错，这道题正是用 BFS 来解的。这道题好就好在限定了棋盘的大小，是 2x3 的，这就让题目简单了许多，由于0的位置只有6个，我们可以列举出所有其下一步可能移动到的位置。为了知道每次移动后拼图是否已经恢复了正确的位置，需要用个常量表示出正确位置以作为比较，那么对于这个正确的位置，还能用二维数组表示吗？也不是不行，但可以更加简洁一些，就用一个字符串 "123450" 来表示就行了，注意这里是把第二行直接拼接到第一行后面的，数字3和4起始并不是相连的。好，下面来看0在不同位置上能去的地方，字符串长度为6，则其坐标为 012345，转成二维数组为：

0  1  2
3  4  5

那么当0在位置0时，其可以移动到右边和下边，即 {1, 3} 位置；在位置1时，其可以移动到左边，右边和下边，即 {0, 2, 4} 位置；在位置2时，其可以移动到左边和下边，即 {1, 5} 位置；在位置3时，其可以移动到上边和右边，即 {0, 4} 位置；在位置4时，其可以移动到左边，右边和上边，即 {1, 3, 5} 位置；在位置5时，其可以移动到上边和左边，即 {2, 4} 位置。

然后就是标准的 BFS 的流程了，使用一个 HashSet 来记录访问过的状态，将初始状态 start 放入，使用一个 queue 开始遍历，将初始状态 start 放入。然后就是按层遍历，取出队首状态，先和 target 比较，相同就直接返回步数，否则就找出当前状态中0的位置，到 dirs 中去找下一个能去的位置，赋值一个临时变量 cand，去交换0和其下一个位置，生成一个新的状态，如果这个状态不在 visited 中，则加入 visited，并且压入队列 queue，步数自增1。如果 while 循环退出后都没有回到正确状态，则返回 -1，参见代码如下：

解法一：

class Solution {
public:
    int slidingPuzzle(vector<vector<int>>& board) {
        int res = 0, m = board.size(), n = board[0].size();
        string target = "123450", start = "";
        vector<vector<int>> dirs{{1,3}, {0,2,4}, {1,5}, {0,4}, {1,3,5}, {2,4}};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                start += to_string(board[i][j]);
            }
        }
        unordered_set<string> visited{start};
        queue<string> q{{start}};
        while (!q.empty()) {
            for (int i = q.size() - 1; i >= 0; --i) {
                string cur = q.front(); q.pop();
                if (cur == target) return res;
                int zero_idx = cur.find("0");
                for (int dir : dirs[zero_idx]) {
                    string cand = cur;
                    swap(cand[dir], cand[zero_idx]);
                    if (visited.count(cand)) continue;
                    visited.insert(cand);
                    q.push(cand);
                }
            }
            ++res;
        }
        return -1;
    }
};

上面的解法虽然很炫，但是有局限性，比如若棋盘很大的话，难道我们还手动列出所有0能去的位置么？其实可以使用最普通的 BFS 遍历方式，就检查上下左右四个方向，那么这样就不能压缩二维数组成一个字符串了，visited 数组中只能放二维数组了，同样的，queue 中也只能放二维数组，由于二维数组要找0的位置的话，还需要遍历，为了节省遍历时间，将0的位置也放入 queue 中，那么 queue 中的放的就是一个 pair 对儿，保存当前状态，已经0的位置，初始时将棋盘以及0的位置排入 queue 中。之后的操作就跟之前的解法没啥区别了，只不过这里新位置就是上下左右，如果未越界的话，那么和0交换位置，看新状态是否已经出现过，如果这个状态不在 visited 中，则加入 visited，并且压入队列 queue，步数自增1。如果 while 循环退出后都没有回到正确状态，则返回 -1，参见代码如下：

解法二：

class Solution {
public:
    int slidingPuzzle(vector<vector<int>>& board) {
        int res = 0;
        set<vector<vector<int>>> visited;
        queue<pair<vector<vector<int>>, vector<int>>> q;
        vector<vector<int>> correct{{1, 2, 3}, {4, 5, 0}};
        vector<vector<int>> dirs{{0, -1}, {-1, 0}, {0, 1}, {1, 0}};
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 3; ++j) {
                if (board[i][j] == 0) q.push({board, {i, j}});
            }
        }
        while (!q.empty()) {
            for (int i = q.size() - 1; i >= 0; --i) {
                auto t = q.front().first; 
                auto zero = q.front().second; q.pop();
                if (t == correct) return res;
                visited.insert(t);
                for (auto dir : dirs) {
                    int x = zero[0] + dir[0], y = zero[1] + dir[1];
                    if (x < 0 || x >= 2 || y < 0 || y >= 3) continue;
                    vector<vector<int>> cand = t;
                    swap(cand[zero[0]][zero[1]], cand[x][y]);
                    if (visited.count(cand)) continue;
                    q.push({cand, {x, y}});
                }
            }
            ++res;
        }
        return -1;
    }
};